Skip to content

Post-quantum decryption based on coding theory

Coding theory, like lattice theory, is a branch of mathematics, and they are intertwined with cryptography

In the fight against quantum computing decryption, coding theory also has its unique development prospects

The more common algorithms in coding theory that have been tried to be used for post-quantum decryption, such as McEliece algorithm, and which be dual with it, is Niederreiter algorithm, the latter has a shorter ciphertext length, but their security level is considered to be the same. Let's take a look at McEliece algorithm

McEliece vs Niederreiter Security Comparison

McEliece Algorithm
↔
Niederreiter Algorithm

McEliece Cryptosystem

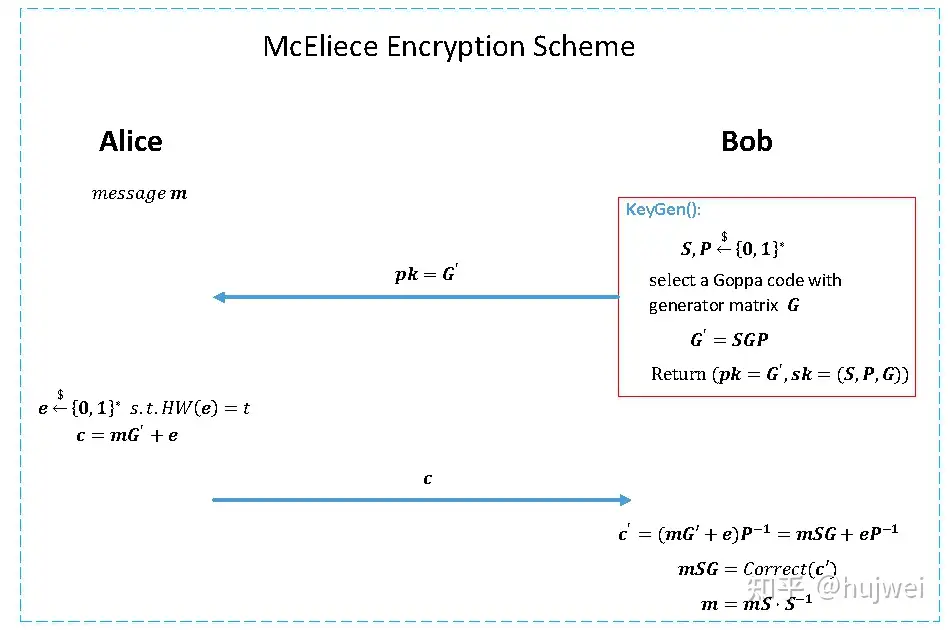
Suppose now Alice wants to send a secret message to Bob. McEliece's idea is this:

Step1. Bob selects linear error correction code Goppa code, and regards the generator matrix \(\mathbf{G}\in\mathbb{F}^{k\times n}\) corresponding to the code as the private key \(sk\), and the public key \(pk\) is the obfuscated version of the generator matrix, that is, \(\mathbf{G'}=\mathbf{SGP}\), where \(\mathbf{S}\in\mathbb{F}^{k\times k}, \mathbf{P}\in\mathbb{F}^{n\times n}\) is a randomly generated matrix (here it is implied that it is difficult to infer \(\mathbf{G}\) given \(\mathbf{G'}\)). The public key \(pk=\mathbf{G'}\) is released to Alice who needs to encrypt information.

Step2. After receiving the public key, Alice performs an encryption operation \(\mathbf{c}=\mathbf{m}\cdot \mathbf{G'}+\mathbf{e}\) on the information \(\mathbf{m}\) to obtain the ciphertext \(\mathbf{c}\) and sends it to Bob.

Step3. After receiving \(\mathbf{c}\), Bob performs a linear operation to obtain \(\mathbf{c'}=(\mathbf{mG'+e})P^{-1}=\mathbf{mSG+eP^{-1}}\). Note that \(\mathbf{P}\) is a randomly generated permutation matrix, with \(HW(\mathbf{e})=HW(\mathbf{eP^{-1}})\), so calling the error correction algorithm yields \(\mathbf{mS\cdot G} \gets Correct(\mathbf{mS\cdot G+eP^{-1}})\), and calling the decoding algorithm yields \(\mathbf{mS}\gets Decode(\mathbf{mS\cdot G})\), which ultimately restores \(\mathbf{m}=\mathbf{mS\cdot S^{-1}}\).

The above encryption and decryption ideas can be expressed by the following figure:

Attacking McEliece

If \(\mathbf{G'}\) does completely hide the structural information of \(\mathbf{G}\), then \(\mathbf{c}=\mathbf{m}\cdot \mathbf{G}+\mathbf{e}\) corresponds to a random linear code (with an error \(\mathbf{e}\)). At this point, the problem of decrypting \(\mathbf{c}\) turns into the problem of how to correct the error of a random linear codeword (Random Linear Code Decoding Problem).

In fact, this problem is NP-hard. The best attack in practice comes from a variant of Information Set Decoding (ISD), and its computational complexity is:

\[ 2^{c_0t(1+o(1))} \]

Here

\[ c_0\approx log\frac{n}{n-k} \]

So as long as the appropriate \(n,k, t\) is set, the attack complexity is exponential. Even in the quantum computer model, using the Grover search algorithm for quantum acceleration, its complexity is about \(\sqrt{2^{c_0t(1+o(1))}}\), which is still exponential.

Note that to ensure the complexity of such an algorithm, or in other words, security, it is necessary to ensure that \(\mathbf{G^{'}}\) does hide the information of \(\mathbf{G}\), that is, it is difficult to infer the valuable information of \(\mathbf{G}\) after \(\mathbf{S},\mathbf{P}\) is obfuscated.

However, in actual operation, even if \(\mathbf{S},\mathbf{P}\) is (pseudo) randomly selected, it does not always play a good obfuscation role. Many linear code selection methods, or confusion matrix generation methods, such as Solomon code, BCH code, etc., cannot hide information well and can be easily cracked by quantum computers.

The \(\mathbf{binary\:Goppa\:code}\) scheme is a method that no one can infer \(\mathbf{G}\) from the obfuscated \(\mathbf{G^{'}}\). The method was given by Shannon Award winner Mceliece, so there is hope that coding theory can be used for quantum-resistant decryption

L(M)DPC scheme

NP-Completed

  • The Goppa code scheme takes advantage of the difficulty of finding Goppa code error vectors with low Hamming weight

  • The MDPC scheme takes advantage of the difficulty of finding low-rank MDPC decoding vectors, which is also related to Hamming weight

Reference